论文阅读-Hadamard Response

标题&地址：Hadamard Response: Estimating Distributions Privately, Efficiently, and with Little Communication
作者：Acharya Jayadev, Sun Ziteng, Zhang Huanyu
发表会议：

---

摘要：本文研究了 $k$ 维频率估计。对于单个用户，已有的方法需要线性的communication，和 $n\cdot k$ 的运行时间，对于较大的 $k$ 不友好。本文提出 Hadamard Response，用户最多只用 $k+2$ bits，运行时间为 $\tilde{O}(n+k)$。

• Introduction
• Preliminaries
  • The privatization mechanisms
  • Previous Results
  • Motivation and Our Results
• A family of $\epsilon$-LDP schemes
• Optimal scheme for high privacy
  • Computational complexity and Hadamard matrices.
• General privacy regimes
• Experiments

Introduction

Distribution Estimation 的目标是给定一个 $k$ 维频率分布 $p$，我们对其估计得到 $\hat{p}$，这个东西本文就简称频率估计了。这当中我们一般会在乎以下几个方面：

• Utility：文中指的是sample complexity的复杂度是多少。其实一般来说utility应当指的是估计的准确率是多少。
• Privacy：我们应当如何去保护用户的隐私。
• Computational Complexity：算法的运行时间是多少。
• Communication Complexity：运行的过程中传输了多少比特。

本文考虑的就是一个结合以上几点的 Distribution Estimation。

Preliminaries

这部分主要说了三个方面：

• Local Differential Privacy：给了LDP的定义。
• Randomness and Symmetry，讲解了一些概念，不必了解也没有关系。
• LDP distribution estimation：相当于problem formulation，讲了什么是基于LDP的。

问题定义：我们可以认为有 $n$ 个用户，每个用户有一个值 $x\in[k]$，然后我们的 groundtruth 就是这 $n$ 个用户的频率直方图（$p$）了。因为要保护隐私，每个用户不能直接发送 $x$，所以要有一个满足 LDP 的机制 $Q$，这样子对于每个用户来说可以这么编码 $z=Q(x)$，服务端收到了 $\mathcal{Z}^n=z_1,z_2,…,z_n$ 之后估计出一个频率分布 $\hat{p}$。可见 $p,\hat{p}$ 都是 $k$ 维向量，那么我们怎么分析误差呢，我们可以用 L1 或者 L2 距离。

The privatization mechanisms

那么当前有哪些方法可以做频率估计呢，主要有以下几个方法：

• k-Randomized Response (RR)：就是KRR的一般情况，其编码方法为：

$$Q_{\mathrm{RR}}(z | x):=\left\{\begin{array}{ll} \frac{e^{\varepsilon}}{e^{\varepsilon}+k-1} & \text { if } z=x \\ \frac{1}{e^{e}+k-1} & \text { otherwise } \end{array}\right.$$

• k-RAPPOR：首先对数据进行一个 onehot 编码，然后对每一位采用 $\epsilon/2$ 进行 randomized response 即可。
• Subset Selection techniques：暂未了解。
• Hadamard Response：就是本文提出的方法。

Previous Results

我们看一下目前方法的问题，首先给出了 sample complexity 如表1所示，不过我好像还没动这个 Sample Complexity 是啥。

然后表2给出了 communication cost，如下：

接着表3给出了运行复杂度：

因为下载的文章没有附录，有一些还不知道作者咋弄过来的。

Motivation and Our Results

简单来说就是收到 hadamard matrix 的启发，设计了 HR 机制。

A family of $\epsilon$-LDP schemes

我们先笼统地介绍一个频率估计机制的 family，步骤如下：

1. 选定 $K$，使得输出空间为 $z\in[K]$
2. 选定 $s < K$
3. 对于 $x\in[k]$，选定定长集合 $C_{x} \subseteq[K]$，其中 $|C_x|=s$
4. 那么从 $[k]\rightarrow[K]$的编码机制可以用以下方程概括：

$$Q(z | x):=\left\{\begin{array}{ll} \frac{e^{\varepsilon}}{s e^{\varepsilon}+K-s} & \text { if } z \in C_{x} \\ \frac{1}{s e^{\varepsilon}+K-s} & \text { if } z \in \mathcal{Z} \backslash C_{x} \end{array}\right.$$

我们可以观察得到 RR 是上述的一个特例，其满足 $K=k,s=1,C_x=\{x\}$。

Optimal scheme for high privacy

直观上来说的话，如果 $x \neq x^{\prime}, C_{x}=C_{x^{\prime}}$，那么我们就不能区分 $x,x’$，进而达到了隐私保护的目的，所以我们设计机制的宗旨就是对于不同的 $x$，我们希望 $C_x$ 尽可能一样。所以我们设计了以下两个目标条件：

C1: 选定 $k<K<2k$，且 $s=K/2$，那么我们有 $|C_x|=K/2$

C2: 对于 $x, x^{\prime} \in[k]$，我们需要满足：$\left|\Delta\left(C_{x}, C_{x^{\prime}}\right)\right|=\left|\left(C_{x} \backslash C_{x^{\prime}}\right) \cup\left(C_{x^{\prime}} \backslash C_{x}\right)\right|=\frac{K}{2}$

我们先不关心如何选择满足这两个条件的参数，作者给出了定理2：

定理2：对于满足C1,C2 的机制，我们有：

$$\begin{array}{l} \mathbb{E}\left[\ell_{2}^{2}(\hat{p}, p)\right] \leq \frac{4 k\left(e^{\varepsilon}+1\right)^{2}}{n\left(e^{\varepsilon}-1\right)^{2}}, \\ \mathbb{E}\left[\ell_{1}(\hat{p}, p)\right] \leq \sqrt{\frac{4 k^{2}\left(e^{\varepsilon}+1\right)^{2}}{n\left(e^{\varepsilon}-1\right)^{2}}} \end{array}$$

那么有了这样的机制之后我们改怎么取基于编码的结果去对频率进行估计呢？我们假设 $Q_{K,\epsilon}$ 是个这样的机制吧。实际上我们很容易证明：

$$\begin{aligned} p\left(C_{x}\right)=& p(x)\left(\sum_{z \in C_{x}} Q_{K, \varepsilon}(z | x)\right)+\sum_{x^{\prime} \neq x} p\left(x^{\prime}\right) \cdot \left(\sum_{z \in C_{x} \backslash C_{x^{\prime}}} Q_{K, \varepsilon}\left(z | x^{\prime}\right)+\sum_{z \in C_{x} \cap C_{x^{\prime}}} Q_{K, \varepsilon}\left(z | x^{\prime}\right)\right) \\ =& p(x) \cdot\left|C_{x}\right| \cdot \frac{e^{\varepsilon}}{\left(s e^{\varepsilon}+K-s\right)}+ \sum_{x^{\prime} \neq x} p\left(x^{\prime}\right)\left(\frac{\left|C_{x} \backslash C_{x^{\prime}}\right| \cdot 1}{s e^{\varepsilon}+K-s}+\frac{\left|C_{x} \cap C_{x^{\prime}}\right| \cdot e^{\varepsilon}}{s e^{\varepsilon}+K-s}\right) \\ =& \frac{1}{2}+\frac{e^{\varepsilon}-1}{2\left(e^{\varepsilon}+1\right)} p(x) \end{aligned}$$

这也就意味着：

$$p(x)=\frac{2\left(e^{\varepsilon}+1\right)}{e^{\varepsilon}-1}\left(p\left(C_{x}\right)-\frac{1}{2}\right)$$

所以就很容易去估计了，也有了以下的算法：

有了这个过程之后，再回过头分析误差就显得自然而然了，具体的计算过程可以参考原文。这里就不再摆出。

Computational complexity and Hadamard matrices

上小节说的是我们只要能选到满足C1,C2的机制，我们就能做到频率估计，那么现在剩下的问题就是如何去选择这样的参数呢？作者想到了 $K\times K$ 的 hadamard 矩阵，对于 $m=2^j$ 的矩阵，这么构造（其中 $H1=[1]$）：

$$H_{m}:=\left[\begin{array}{cc} H_{m / 2} & H_{m / 2} \\ H_{m / 2} & -H_{m / 2} \end{array}\right]$$

hadamard 矩阵有着以下几个特点：

• 除了第一行，每一行的1的个数都是 $K/2$
• 任意两行刚好有 $K/2$ 个位置相同
• 乘法计算复杂度可以为 $O(K \log K)$
• 每一行的随机采样复杂度为 $O(\log K)$

那么我们可以这么选择满足 C1, C2 的参数：

• 选择 $K$: $K=2^{\left\lceil\log _{2}(k+1)\right\rceil} \geq k+1$，即 $K$ 为 比 $k$ 大的最小的2次幂。
• 选择 $C_x$: 对于值 $x$，$C_x$ 为 hadamard 矩阵第 $x+1$ 行的 1 对应的位置。

注意，为了实现这个机制，我在自己偷懒在网上查生成 Hadamard Matrix 的代码是有问题的，如果读者复现的过程出现了问题，有可能是这里导致。

那么到这里差不多就介绍完了。

Experiments

参数选择如下：

• $k \in\{100,1000,5000,10000\}$
• $n \in \{50000,100000,150000, \ldots, 1000000\}$
• $\epsilon \in\{0.1,0.5,1,2,3,4,5,6,7,8,9,10\}$
• 数据分布有 geometric 分布，zipf 分布， two-step 分布和 uniform 分布。

然后对于每个机制，运行30轮，取了平均 L1 error。

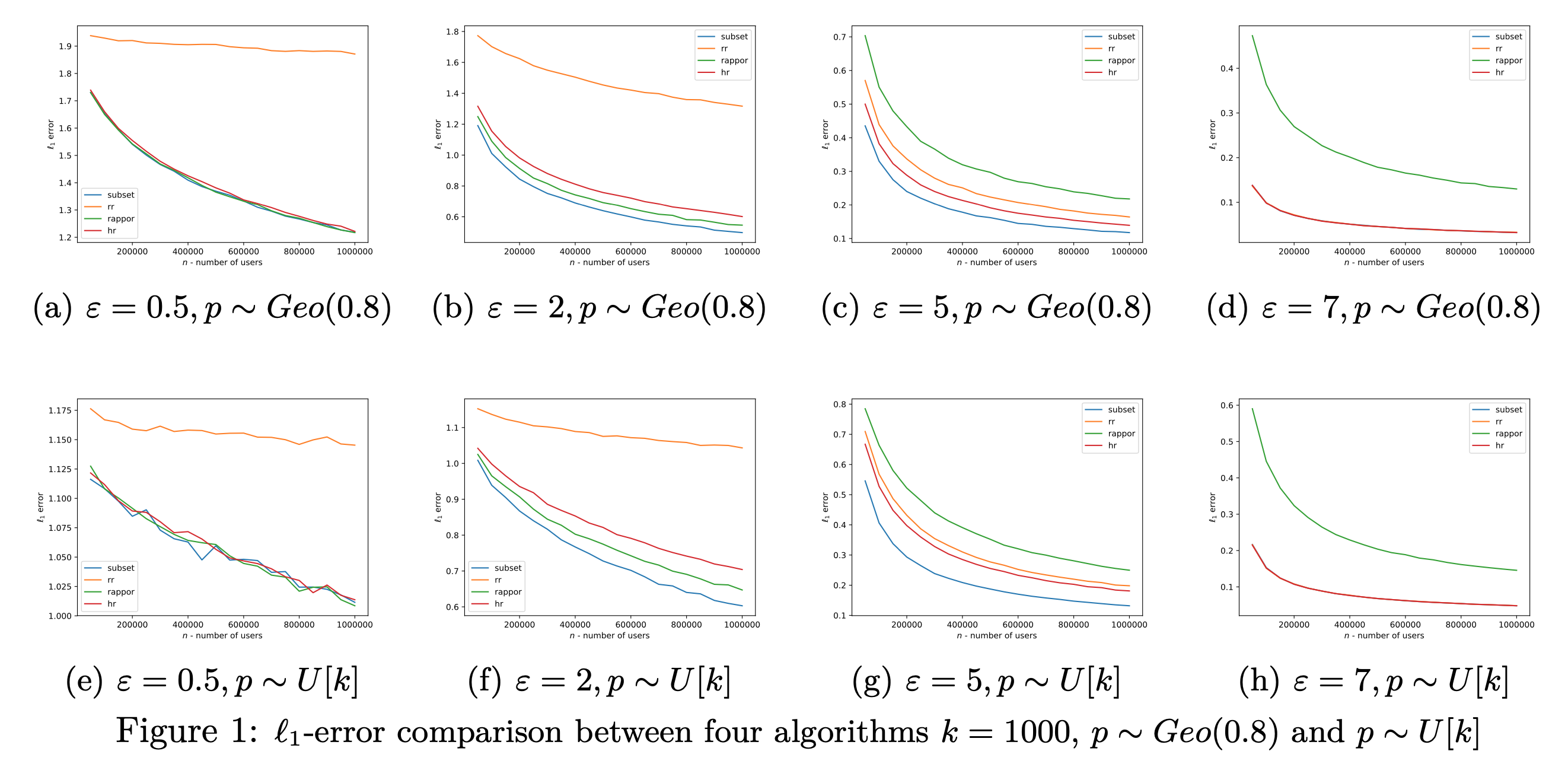
图1毙了 $k=1000$ 的情况。总的来说差不多还是 subset 这个方法效果最好了。

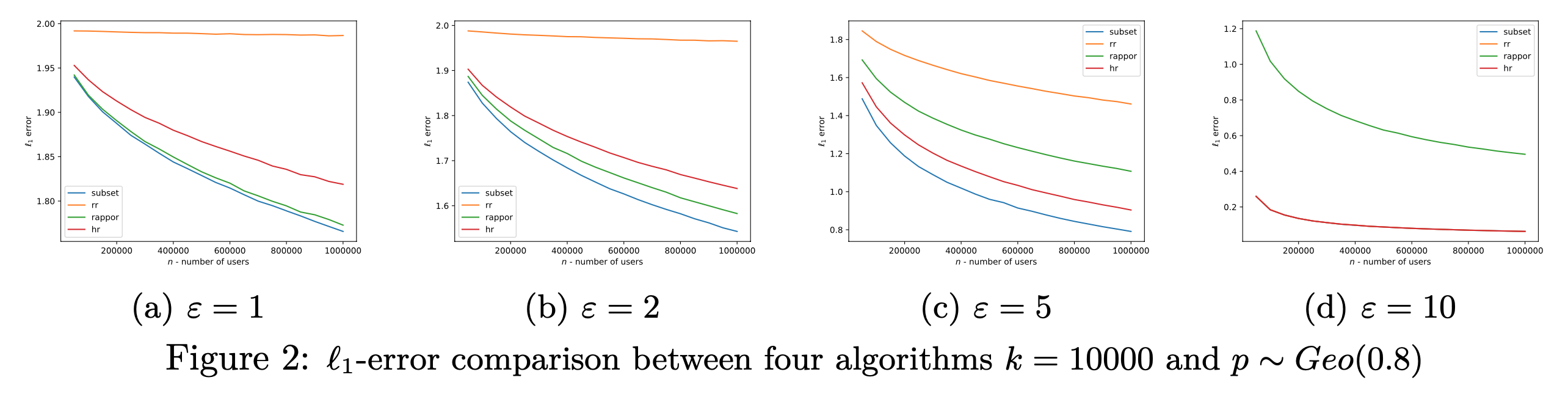
图2毙了 $k=10000$ 的情况，可以看到的是如果 $k$ 太大了，那么 RR 效果就不好了。

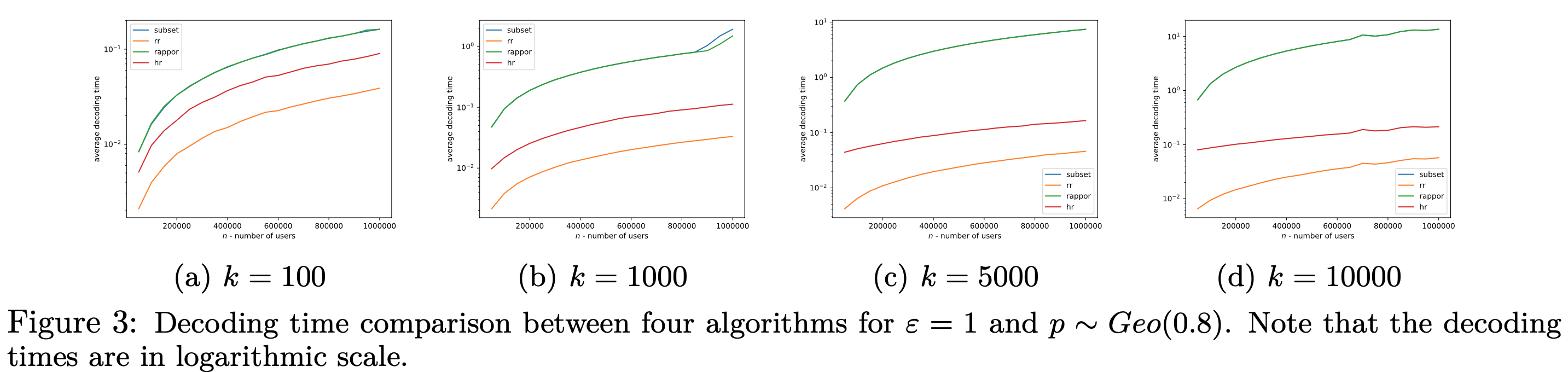
总的来说就是 subset 这个方法可能效果比较好，但是运行时间慢，rr呢运行快，但是效果不是很好，然后呢我们的方法可以有一定的折中。

---

本篇内容到这里就结束了，欢迎关注公众号《差分隐私》，获取更多前沿技术。